Evolution of an Equation: From Superluminal Shadows to Private Vector Search

TL;DR

A simple geometry demo—a shadow edge outrunning light—grew into a portable similarity system.

v1 (Origin): Multiplicative, interpretable similarity born from a shadow’s “gain × angles × rate.”
v2.1 (Canonical): One ARD-Mahalanobis quadratic + bounded exponential, wrapped in a production GP/BO stack.
v3.0 (FHE): Two-stage private vector search—low-rotation CKKS recall, then plaintext re-rank for fidelity.
Code + OSF below.

In 2024 I posted a thought experiment: a point light, a rod, a tilted screen. The shadow edge on the screen can sweep faster than c because no object or signal travels along that edge—it’s just a geometric locus moving across a surface.

I wrote it roughly as:

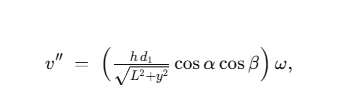
i.e. (projected lever-arm) × (angular rate), scaled by the geometry. The point wasn’t to reinvent relativity; it was to make apparent superluminality intuitive and to capture the structure: scale × distance × orientation × dynamics.

Original blog (May 23, 2024): https://hmwh.se/blog/2024/05/23/breaking-the-speed-of-light-with-shadows/
Background OSF: https://osf.io/gk45m/

2) Abstraction: from optics to embeddings

The geometry rhymed with vector similarity. So I transplanted the pieces:

$h \to ∥ v ∥$ (state strength)
$d_{1} \to$ distance to a reference/centroid
$\sqrt{L^{2} + y^{2}} \to dataset scale/offset$
$α, β \to$ orientation/importance angles
$ω \to dynamics/time weight$
extra $γ_{i} \to$ feature-wise alignments with weights wi

Version 1 became an interpretable, multiplicative θ‴: a product of factors whose meanings were obvious. That made it portable: trading, behavior/safety, creative rhythm analytics, hypersonic sensing, governance/HFT experiments—you name it. It also surfaced a few pain points: manual weights, scale coupling, and post-hoc normalization.

v1 OSF: https://osf.io/d4bwg/

3) Consolidation: θ‴ v2.1 (the canonical form)

I refactored the multiplicative score into one ARD-Mahalanobis distance over dimensionless, soft-clipped features, then used a bounded exponential similarity:

1: Encode & normalize
Continuous passthrough, periodic $[sin θ, cos θ]$ (optionally $∣ θ - θ^{\*} ∣$ ) , categorical via learned embeddings rescaled to unit variance, plus context/time as features. Normalize by per-feature $σ_{i}$ (IQR-based) and soft-clip deltas with a tanh clamp to keep gradients tame. Freeze $σ$ after one guarded re-estimation (prevents $σ / ℓ$ drift).

2: Distance & similarity

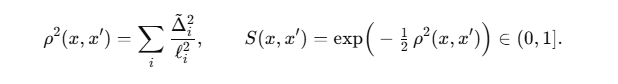
No cosine stacks, no extra $ω$ , no post-hoc $N$ . Angles and dynamics live as features, and ARD learns what matters.

3: Production GP/BO stack
Deterministic runs (seeded fantasies, pinned threads), jitter escalation, heavy-tail options (Student-t/Huber), constraints via PoF, qNEI ↔ qEI hysteresis on observed noise, async + dedup + replicates, OOS validation, full logging.

v2.1 OSF: https://osf.io/q6eug/
Code (theta3bo): https://github.com/HMarcusWH/theta3bo

Why it matters: same intuition, clean math (PSD-safe), learned importance instead of hand-tuning, and operational guarantees that scale beyond demos.

4) Privacy by design: θ‴ 3.0 (FHE)

The canonical quadratic is also the cheapest thing to do under CKKS. Version 3.0 turns that into a two-stage private vector search:

Stage A — Encrypted recall (CKKS): rank the entire corpus using an ARD-weighted quadratic in a reduced space ( $p^{'} \sim 16 - 64$ ) with low-rotation packing. Optional client-norm piggyback removes the ciphertext×ciphertext multiply. No bootstrapping.
Stage B — Plaintext re-rank: reorder the top-K (e.g., 64–256) with either the legacy multiplicative razor (maximum fidelity) or v2.1 again—or a small domain model.

This split gives better Recall@K than encrypted L2 at the same HE budget, while keeping latency predictable and ops deterministic. It’s the natural endgame of the equation’s evolution: cheap private recall, sharp public precision.

v3.0 OSF: https://osf.io/r2c5h/

5) What we actually brought to the table

Not a brand-new equation—a system:

A design pattern (strength × distance × orientation × dynamics) that stays interpretable across domains.
A canonical core (v2.1): ARD-Mahalanobis over dimensionless, soft-clipped features—stable, learnable, PSD-friendly.
A production BO engine around it (constraints, heavy-tails, hysteresis, async, reproducibility, audit logs).
A privacy-preserving search architecture (3.0): low-rotation CKKS recall + plaintext re-rank, no bootstrapping, with acceptance gates tied to Recall@K.
Cross-domain recipes: materials (nickelates, twistronics, SDEs), SEO/ads, systematic trading, safety/behavior, sensing, creative analytics.

6) Resources (timeline)

Origin blog: https://hmwh.se/blog/2024/05/23/breaking-the-speed-of-light-with-shadows/
OSF origin notes: https://osf.io/gk45m/
Version 1 (multiplicative start): https://osf.io/d4bwg/
Version 2 (θ‴ v2.1 + BO): https://osf.io/q6eug/
GitHub (theta3bo): https://github.com/HMarcusWH/theta3bo
Version 3 (θ‴ 3.0, FHE): https://osf.io/r2c5h/

7) What’s next

Benchmarks: publish Recall@K vs encrypted L2 (3.0), and uplift vs cosine/L2 baselines (v2.1) across 2–3 datasets.
Cookbooks: one runnable notebook per domain (materials, SEO/ads, trading), plus HE rotation/key budgets for $p^{'} = {16, 32, 64}$ .